Memorize These SAT Math Tips, Tricks, Formulas, and Concepts
There Is No Substitute for Memorization in SAT Math
Do you want a higher SAT Math score and rock-solid confidence on test day? Learn about the best SAT math book in the world!
Students hate memorization, especially memorization of mathematical formulas and concepts. But all facts you “know” are facts you’ve memorized. You’ve thought them, said them, engaged with them so much that they’ve become second nature, part of your body of knowledge, stored in your long-term memory. If you want to do well on the SAT Math section, you MUST memorize these formulas and concepts. I wrote this list from scratch. How? I’ve memorized it.
If you want to succeed on the SAT and ACT, and if you want your SAT and ACT prep lessons to be as useful as possible to you, you’re going to need to memorize facts, rules, and formulas. You’re also going to need to know why the facts, rules, and formulas are what they are, and how to apply them.
If you’re the type of student who learns a concept or formula and is told to memorize it but returns to class WITHOUT having memorized it, why are you even in class to begin with? People who refuse to memorize facts they KNOW they will need are lazy, plain and simple. It’s a hard truth. Even IF you memorize the formula/concept, you have to make sure to ACCURATELY apply it.
Here’s a good way to memorize mathematical formulas. Memorize them as both TEXT and IMAGE. Convert them into TEXT. Memorize the TEXT by saying it out loud to yourself and copying it out as a mathematical formula as you do so. Before you take the SAT, drill yourself on these formuals and concepts. There is no substitute for memorizing them.
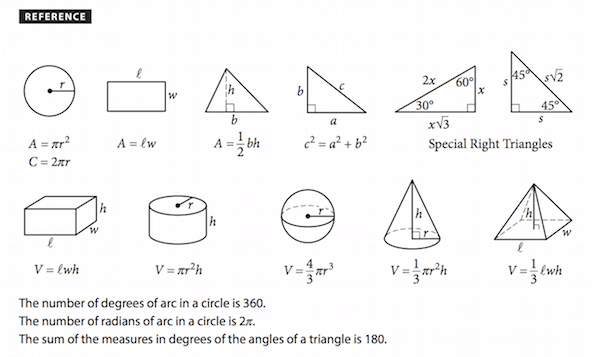
Take a look at the formula chart you’re given for the SAT math section. It is WOEFULLY inadequate. It contains none of the information that follows it, and you need to MEMORIZE this information.
What are some things you need to memorize for SAT Math?
The slope formula
If you have the coordinates of two points, to calculate the slope of a line, use the following formula:
“Y two minus Y one over X two minus X one.”
The distance formula
“Distance is the square root of Y two minus Y one squared plus X two minus X one squared.”
Distance is exactly the same as the Pythagorean theorem, where the distance between two points is the hypotenuse of a right triangle.
The midpoint formula
If you have coordinates for two points, calculate the midpoint by averaging the x coordinates and averaging the y coordinates.
The quadratic formula
The quadratic formula can be used to find the X-intercepts of a parabola:
“Negative b plus or minus the square root of b squared minus 4ac all over 2a.”
How to get the X-coordinate of the vertex of a parabola in standard form:
“Negative B over 2A”
If you need the Y-coordinate of the vertex, plug the X-coordinate you got into the equation.
The X-coordinate of the vertex of a parabola in factor form
The MIDPOINT of the X-intercepts is the X-coordinate of the vertex of a parabola in factor form. If you need the Y-coordinate, plug the X-coordinate you got into the equation.
Sum of the solutions (x-intercepts, zeroes) to a parabola
Negative B over A.
Number of radians in a circle
There are 2 Pi radians in a circle.
Converting degrees into radians
Degrees times Pi/180.
What the word “factor” means
A parabola in factor form looks like (X-3)(X-2). It means that the parabola has X-intercepts of 3 and 2. If it were (X+3)(X+2) the x-intercepts would be -3 and -2. If they ask you for a factor, you’re looking for the place where Y = 0.
Percent change
(Old - new) / (old)
This will give you a decimal, so be sure to convert it into a percentage (multiply by 100). Another way to memorize this is “Difference over original.”
Mean, Median, Mode, and Range
Mean = Sum / Number
Median = Middle number when data is arranged least to greatest
Mode = most common data point
Range = High number minus low number
SOHCAHTOA
Sin = opposite over hypotenuse
Cos = adjacent over hypotenuse
Tan = opposite over adjacent
How to FOIL
When you multiply two binomials, you need to use FOIL. It stands for First Outside Inside Last.
For example:
(X+2)(X+3)
First: X times X
Outside: X times 3
Inside: 2 times X
Last: 2 times 3
Then combine terms.
How to Factor
When you have a parabola in standard form (ax squared plus bx plus c) and want it in factor form, you must factor.
For example:
X^2 + 5x + 6
You need to choose factors that ADD to the middle term and MULTIPLY to the last term.
What adds to 5 and multiples to 6. 2 and 3.
So the factored form for the above equation is (x+2)(x+3).
What “i” is
i is an imaginary number. It’s always the square root of negative 1.
What “i squared” is
i^2 = -1
How to do problems with imaginary numbers
Multiply the numerator and denominator by the conjugate of the denominator over the conjugate of the denominator.
For example:
3-5i/8+2i
Multiply it by 8-2i / 8-2i. Don’t forget to FOIL. Substitute the i-squareds you produce with -1. Combine terms. Reduce if possible.
Difference of squares
Be able to recognize a difference of squares. They’re incredibly easy to factor.
For example:
x^2 - 16 = (x-4)(x+4)
x^2 - 64 = (x-8)(x+8)
x^2 - y = (x - root y)(x + root y)
Exponent rules
x^2 times x^3 = x^5
x^6 divided by x^2 = x^3
(x^2)^3 = x^6
x^-1 = 1/x
x^(2/3) = cubic root of x^2
The discriminant
The discriminant is the b squared minus 4ac part of the quadratic formula. If the discriminant is negative, parabola has 0 real solutions. If it equals 0, parabola has one real solution. If it’s positive, parabola has 2 real solutions.
Equation of a line
y = mx + b
If the line isn’t in this format, put it in this format. Y is the output variable, X is the input variable, M is the slope (rate of change) and B is the y-intercept. If you know a point and a slope, you can get the equation of a line. If you know two points, you can get the equation of a line. Simply plug in what you know into the y = mx + b formula and use algebra to solve for an unknown.
Lines can be tables, graphs, or equations
Be able to get the equation of a line from a table of values. How? Use the points to calculate slope, then use points and the slope and algebra with y = mx + b to calculate the y-intercept.
When a system of equations has “solutions”
A solution to a system of equations is the point at which the lines cross. If they don’t cross, they’re parallel. Parallel lines have the same slope. A system with one solution crosses once, two solutions crosses twice, INFINITE solutions are the SAME equation, and NO solutions means they never cross.
Solving a system of equations
Substitution = solve for one variable and plug into the other equation.
Otherwise, elimination. You can multiply either of the equations by whatever you need to add the equations together in a way that eliminates a variable.
The whole philosophy behind solving systems of equations is the whole philosophy of algebra. Namely, you can find ONE unknown if you know the rest of the equation.
Corresponding coefficients in equivalent polynomials
When you’ve got a polynomial like x^2+14x+c set EQUAL to another polynomial, like (X+d)^2, you have to understand that they are the SAME polynomial. They’re equal. So put them in the same form and find unknowns by setting coefficients equal to one another. In this example, you’d FOIL out the polynomial on the right, getting X^2 + 2dx + d^2 = x^2+14x+c, meaning 2d=14 and c = d^2, meaning d=7 and c=49.
Percent
Part over whole times 100.
Probability
Desired outcome / possible outcomes
Be careful on tables with multiple data points. Ask yourself: what do we want? What are we choosing from?
PEMDAS - Order of Operations
PEMDAS is a hugely important acronym that tells you the proper order in which to perform mathematical operations, and it stands for Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. If you don’t properly perform perform operations in this order, you’ll get an incorrect answer, and guess what? The SAT probably has that incorrect answer listed as an answer choice designed to trick you! Related to PEMDAS is the order in which you UNDO things in algebra, SADMEP.
* * *
Now that you’ve reviewed some key SAT Math formulas, it’s time to take the next step. Get your hands on the best SAT Math prep book ever written!
That’s it! For more SAT and ACT prep tips, check out the rest of our blog. Looking for 1-on-1 ACT or SAT prep tutoring? Want to join an SAT or ACT group class? Contact us today!
