Do you want a higher SAT Math score - including total confidence on all SAT questions involving Imaginary Numbers? If so, check out the best SAT Math prep book ever written!
Imaginary Numbers on the SAT
SAT math has never been easy–in fact, it’s developed a relationship for being quite tricky. One of the most common reactions I get when showing students how to solve a tricky SAT problem is “We never learned that in school!” Well, hopefully your school is teaching you how to handle imaginary numbers, because the SAT certainly tests you on them–and on the NO CALCULATOR math section, no less! Here, I’ll guide you through a typical SAT imaginary number problem.
First off: What IS an imaginary number?
An “imaginary number” is a complex number that can be defined as a real number multiplied by the imaginary number i. i is defined as the square root of negative one. If you’ve taken basic math, you know that the square of every real number is a positive number, and that the square root of every real number is, therefore, a positive number. But not with imaginary numbers! In the realm of imagination, it’s totally possible to square a number and get a negative answer!
Basically, what you need to know is:
i = the square root of negative one
i squared = negative one
With this knowledge, you’ll be prepared to handle imaginary number questions on the SAT!
Let’s learn how to do an imaginary number problem on the SAT
All right, now that we’ve defined the term “imaginary number,” we’re ready to handle a problem with imaginary numbers on the SAT. Most often what they want you to do is to simplify a division expression containing imaginary numbers. It’s important to practice this exact operation, so pay close attention!
Here’s the problem:
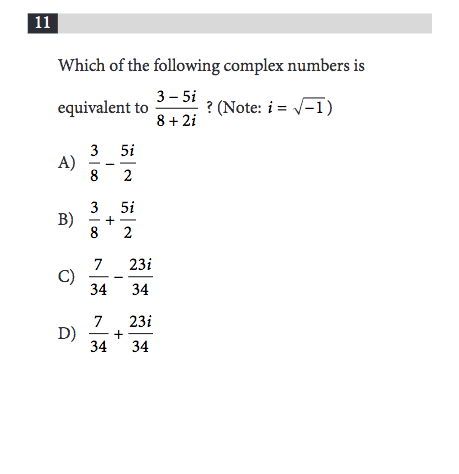
Any idea how to solve the problem? If not, that’s totally okay! That’s what we’re here for. First off, let me outline the basic process by which we’re going to solve the problem.
Step one: Multiply the numerator and denominator of this ugly fraction by the CONJUGATE of the denominator. What’s the conjugate, you ask? It’s the same thing as the denominator with one critical difference: the sign in the middle gets flipped! In this problem, the denominator is 8+2i, so the conjugate is 8-2i.
Step two: Replace all instances of i^2 with -1. Remember how we said that i^2 is equal to -1? This is why that’s useful!
Step three: Reduce (simplify) the result, if possible.
Easy as one, two, three, right? Let’s solve the problem!
Step one: Multiply the numerator and denominator by the conjugate
We’re going to multiply this fraction, 3-5i / 8+2i, by the conjugate. That means we’re going to multiply the original fraction by 8-2i / 8-2i.
Why are we allowed to do this? Because 8-2i / 8-2i equals one. Anything over itself equals one. We’re not changing the VALUE of the expression…we’re simply changing its FORM. And we’re totally allowed to do this.
The thing to be aware of during this step is to make sure you FOIL properly. When you multiply two binomials, it’s critically important that you FOIL. FOIL stands for First, Outer, Inner, Last, and it’s there to remind you which terms to multiply when multiplying binomials.
When we FOIL the numerators (3-5i)(8-2i) we get 24 - 6i - 40i + 10i^2. Combining terms, this gives us 24 - 46i + 10i^2.
When we FOIL the denominators (8+2i)(8-2i) we get 64 + 16i - 16i - 4i^2. Combining terms, this gives us 64 - 4i^2.
Step two: Replace occurrences of i^2 with -1.
Easy, right? Just be careful not to screw up negative signs!
Replacing all instances of i^2 with negative one in the new numerator gives us 21 - 46 - 10(-1). Combining terms, this gives us 14 - 46i.
Replacing all instances of i^2 with negative one in the new denominator gives us 64 - 4(-1). Combining terms, this gives us 68.
So our new fraction is 14 - 46i / 68. Which brings us to step three…
Step three: Reduce the fraction if possible!
All of the numbers in the fraction are divisible by 2, so the fraction reduces to 7 - 23i / 34. It’s totally possible to split this fraction into the difference of two fractions, or 7/34 - 23i/34. And that’s answer choice C!
Hooray! We solved the problem correctly!
Learn this process well. It will enable you to handle the tricky imaginary number questions on the SAT!
* * *
For more practice and confident mastery of imaginary numbers on the SAT Math test, check out SAT Math Mastery Volume 2 - the second volume of the best SAT Math textbook ever written! It covers imaginary numbers in great detail, along with 18 other crucial lessons for the SAT Math test.
That’s it! For more SAT and ACT math tips, check out the rest of our blog. Looking for 1-on-1 ACT or SAT prep tutoring? Want to join an SAT or ACT group class? Contact us today!
