Most students are intimidated by trigonometry when they’re first exposed to it, and this need not be the case. If you’re worrying about trigonometry on the ACT, you shouldn’t be–for one thing, there are only three or four trig problems on the ACT. And they’re easy once you know how to solve them! Here, I’ll teach you how to solve a difficult trig problem from a real ACT.
First off, though, a refresher on some basic trig concepts.
SOHCAHTOA
The first thing to know about trigonometry is that sine, cosine, and tangent are RATIOS. Each of the two complementary angles of a right triangle (i.e. the two angles that add up to 90 degrees) has a sine, cosine, and tangent. To figure out the sine, cosine, and tangent of an angle, you can use the SOHCAHTOA acronym.
SOH means that sine = opposite over hypotenuse. Take the side length opposite from your angle and put it over the side length of the hypotenuse. Then you’ve got your sine ratio!
CAH means that cosine = adjacent over hypotenuse. Take the side length adjacent (next to) your angle and put it over the side length of the hypotenuse. Then you’ve got your cosine ratio!
TOA means that tangent = opposite over adjacent. Take the side length opposite from your angle and put it over the length of the side that’s adjacent to your angle. Then you’ve got your tangent ratio!
Easy, right? Do NOT forget SOHCAHTOA or how to use it. It will come in handy on literally every ACT trig problem.
The Unit Circle
The Unit Circle looks scary and confusing to many students, but if you know a few basic things, it’ll be easy for you to understand it and use it on tricky trig problems. First of all, it’s important to know that the are 360 degrees in a circle. There are also 2 Pi radians in a circle. Degrees and radians are just different ways of measuring angles. To convert from degrees to radians, multiply the number of degrees by Pi/180. The unit circle can be labeled with infinitely many measurements of radians, but if you know 4 basic points and understand fractions, it should be no problem for you to see where other measurements would be. Here’s a graphic:
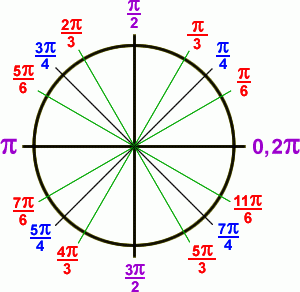
Frankly, you do not need to memorize every single measurement in this graphic. You need to know four basic measurements and use common sense and knowledge of fractions to figure out where other measurements might fall. The four measurements you need to know are the ones in purple above. The unit circle starts at 0 and goes counterclockwise and ends up at 2 Pi. (Remember, there are 2 Pi radians in a circle!) At the 90 degree mark, you have the Pi / 2 measurement. Then, at the 180 degree mark, you have Pi. (Makes sense, right, because if 2 Pi is a circle, then Pi is half of a circle.) Then at the 270 degree mark, you have 3 Pi / 2. And finally, at the 360 degree mark, the same place the unit circle began, you have 2 Pi, bringing the circle to a close. If you have common sense, you’ll know that 3/4 Pi is between Pi / 2 and Pi, because 3/4 is between 1/2 and 1. So you don’t need to memorize a million fractions if you know the four basic measurements on the unit circle.
All Students Take Calculus
Once you have a basic understanding of the unit circle, you’re ready to learn an INCREDIBLY useful mnemonic device that can help you eliminate 2 answer choices on a tricky trig problem, bringing your odds of GUESSING the right answer to 50/50. But you won’t need to guess, because the proble will be a piece of cake after this tutorial. The mnemonic device in question is ALL STUDENTS TAKE CALCULUS.
It tells you which of the trigonometric ratios is POSITIVE in any given quadrant.
ALL goes in Quadrant I. It means that in Quadrant I, sine, cosine, and tangent are all positive.
STUDENTS goes in Quadrant II. It means that only sine is positive in Quadrant II. Cosine and tangent are negative.
TAKE goes in Quadrant III. It means that only tangent is positive in Quadrant III. Sine and cosine are negative.
CALCULUS goes in Quadrant IV. It means that only cosine is positive in Quadrant IV. Sine and tangent are negative.
Amazing, right? Do NOT forget All Students Take Calculus. It will be a life-saver on the ACT Math section, at least as far as the tricky trig problems are concerned!
Tricky Trig Problem Made INCREDIBLY Easy
Let’s put what we learned into practice as we tackle the following ACT trig problem.
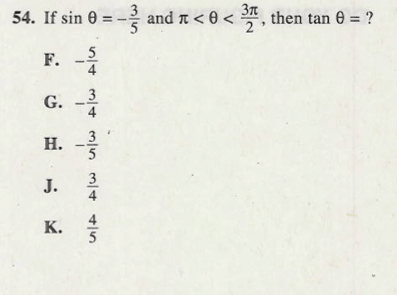
Notice that it’s problem 54, and since ACT math questions go roughly in order of difficulty, it’s a HARD problem. It won’t be so hard now! Here’s how to solve it.
First of all, that symbol is THETA, a Greek letter used to refer to an angle. Basically, the problem is saying that there’s an angle in a triangle that has a sine of -3/5. Then it’s saying that the angle in question is between Pi and 3/2 Pi. Remember the Unit Circle above? Which quadrant does that mean the angle’s in?
Since the angle is between Pi and 3/2 Pi, that means the angle is in Quadrant III.
What do we know about Quadrant III, given that ALL STUDENTS TAKE CALCULUS?
We know that in Quadrant III, only the TANGENT is positive. And guess what? This problem wants the TANGENT of the angle.
That means we can eliminate answers F, G, and H, since they’re all negative! How easy. Now the answer is either 3/4 or 4/5. No need to guess, though–it’s easy to solve!
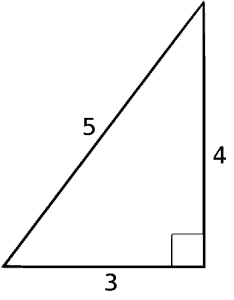
Draw yourself a right triangle. Let one of the angles have a sine of -3/5, meaning that the side opposite the angle is 3 and the hypotenuse is 5. You should know that you’re dealing with a 3-4-5 right triangle, making the adjacent side 4. What’s the tangent of the angle?
It’s 3/4. Easy.
The correct answer is J.
Remember that trig on the ACT is NOT as bad as you think it is. With a few basic concepts, such as SOHCAHTOA, the Pythagorean theorem, All Students Take Calculus, and the Unit Circle, you’ll be getting the tricky trig questions correct in no time!
* * *
That’s it! Hope this helps. For more ACT prep tips, check out the rest of our blog. Looking for 1-on-1 ACT or SAT prep tutoring? Want to join an SAT or ACT group class? Contact us today!