SAT Geometry Problems: Tips and Tricks
Having been an SAT and ACT prep tutor for several years now, I’ve noticed a recurring comment among my students whenever they encounter difficult geometry problems on the SAT math test (in both the no-calculator and calculator-allowed sections). “Man, geometry was so long ago,” they say. “I’m worried I’ve forgotten how to do this problem.” While it’s true that most students take geometry their freshman year of high school and that most SAT prep students are juniors and seniors engaged in Algebra II, Pre-Cal, or even Calculus, a well-kept secret concerning the SAT math test’s geometry problems might just allow students such as these to tackle difficult geometry problems with ease. The secret? Geometry problems on the SAT math section are really (often) algebra problems in disguise. Though knowledge of certain geometric properties and formulae offer students an entry point into the problem in question, a surefire way to solve said geometry problem is to turn it into an algebra problem.
Why is it possible to turn SAT geometry problems into algebra problems?
Before we discuss just how much geometry is on the SAT and list some common geometry topics the SAT math section tests, let’s examine the question of why it’s even possible to turn SAT geometry problems into algebra problems. After all, they sure look like geometry problems, containing diagrams of lines, triangles, circles, solids, and so on.
The thing to understand, however, is that each SAT question asks students to discover an unknown. One’s task might be to find the length of a given arc of a circle, for example, knowing only the length of the circle’s radius and a degree measure of the arc in question. Though this certainly looks like a geometry problem, it’s really solvable using algebra. The secret? Setting up a proportion: degree measure over three-sixty equals X over circumference. Solve the proportion for X and you’re done. Of course, successful completion of a problem such as the one I’ve just mentioned requires a student to 1) know that circles are character by proportional relations, 2) know the formula for circumference of a circle, and 3) know how to set up and solve a proportion.
The formula chart the SAT math sections (no-calculator and calculator alike) provide to students contains the circumference formula, but it neglects to mention that relationships in a circle are proportional. If you worry about forgetting a geometry formula on the SAT, you might be in luck, as the formula chart does indeed contain many helpful formulas concerning the area, perimeter, and volume of two-dimensional and three-dimensional shapes respectively. However, there are many things the SAT math formula chart does NOT contain, so it’s vital that you’re able to recall concepts and formulas that aren’t on the formula chart if you hope to succeed on SAT geometry problems.
How much geometry is on the SAT?
Students who prefer algebra to geometry should rejoice to know that geometry problems can be turned into algebra problems on the SAT. They should further rejoice to know that there aren’t that many geometry problems on the SAT to begin with. The test is deeply, heavily algebra-focused. Geometry comprises about 10% of the math problems on the SAT. The rest involve algebra, statistics, and data analysis.
In terms of what to prioritize when studying for the SAT, then, it makes sense to first ensure you have a very strong fluency in algebra and statistics and data analysis. Strong algebra skills (understanding concepts, setting up and solving equations) are a must for success on the SAT math section, even, as we shall see, when it comes to the 10% of SAT math problems that focus on geometry.
What geometry topics does the SAT test?
What sort of geometry topics does the SAT math section want you to know? The list is fairly straightforward.
On the SAT no-calculator and calculator math sections, students might encounter geometry questions that…
1) ask them to solve for an unknown using volume formulas
2) use trigonometric ratios and/or the Pythagorean theorem to find unknowns (usually side lengths or angles) in right triangles. They also love the complementary angles property of sine and cosine, which states that when x+y=90, sin(x)=cos(y) and vice versa.
3) convert between degrees and radians (this is NOT on the formula chart, so it’s important to memorize that degrees times Pi over 180 equals radians) and use either degrees or radians to determine arc length
4) use circle formulas and theories to find arc length, chord length, angle measure, and sector area of a circle
5) use the geometry concepts of congruence and similarity to determine information about lines, angles, and sides in geometry figures
6) create or use the circle equation to solve problems concerning circles in the coordinate plane. Again, note that information on the equation of a circle is NOT on the formula chart, so it’s important to know that the equation for a circle should be in the form (x-h)^2 + (y-k)^2 = r^2 and that if the the circle isn’t in this form it’s wise to put it in this form by completing the square (another process you’ll need to memorize and practice)
And that’s it! There are pretty much 6 geometry topics on the SAT, and all of them involve using algebra to solve for unknowns. Let’s take a look at some of these problems and how you can use algebra to solve them.
Strategy in action: turning SAT geometry problems into algebra problems
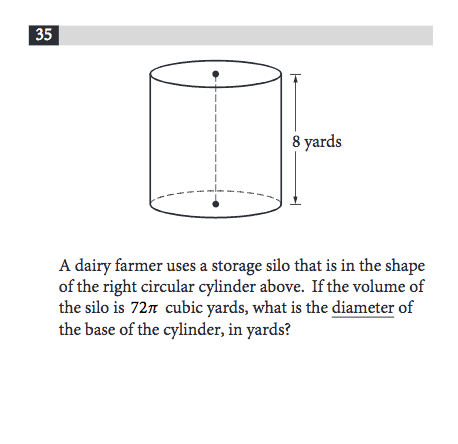
In the problem above, you’ll need to use the formula for the volume of a circle. The unknown you’re solving for is the circle’s diameter.
Pi R^2 H is the formula for the volume of a circle. You know the volume, Pi, you know the height is 8 yards, so set up your equation and solve for R.
Pi R^2 (8) = 72pi.
Dividing both sides by pi gives R^2 (8) = 72.
Dividing both sides by 8 gives R^2 = 9.
Square rooting both sides gives R = 3.
And the problem wants diameter, which is twice the radius, so 3*2 = 6, making the answer 6.
Notice how we used knowns to solve for an unknown? That’s algebra!
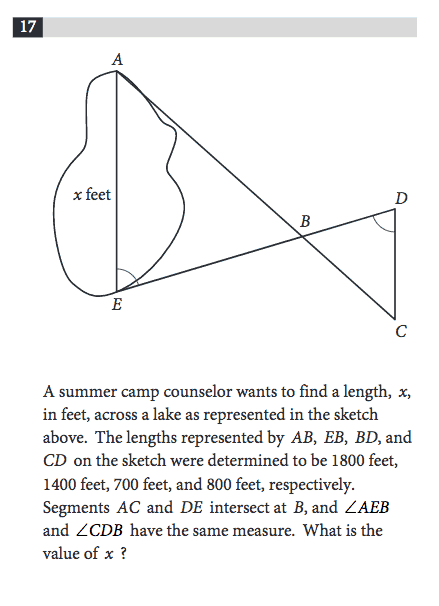
In this next problem, we’re dealing with triangles. If you see triangles on the SAT, there’s a good chance you’ll be dealing with concepts of congruence or similarity. How to recognize when you’re dealing with similar triangles? Similar triangles have identical angle measures and, accordingly, proportional side lengths.
The problems tells you that angle AEB and angle CDB have the same measure. That fact, combined with the fact that angles CBD and ABE are vertical angles (and thus also have the same measure) is enough information for you to discern that all 3 angles of the two triangles have the same measure. Hence, their side lengths are proportional.
Let’s set up a proportion and use algebra to solve.
700/1400 = 800/x.
Cross multiplying and dividing reveals that x = 1600.
Not so bad!
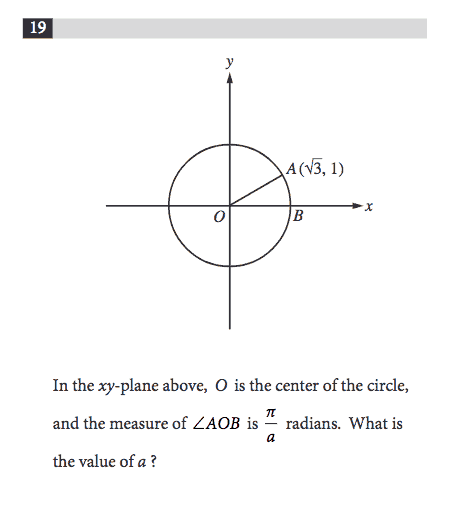
The problem above requires you to convert from degrees to radians, but other than that, you don’t really need to know much about radians or the unit circle. Students doing well in pre-Cal tend to get this problem quickly, but it’s actually solvable using geometry and algebra.
The thing to recognize is that the point (root 3, 1) tells you the dimensions of a right triangle. The length of its two legs? Root 3 and 1. Seeing root 3 on a triangle is a huuuuge tip-off. They want you to recognize that you’re dealing with a 30-60-90 triangle. The ratios of the side lengths for a 30-60-90 triangle can be found on your formula chart. When you consult it, you see that across from the 30 degree angle is the smallest side (in this case, 1); across from the 60 degree angle is the second-biggest side (in this case, root 3); finally, across from the 90 degree angle is the hypotenuse (in this case, using either 30-60-90 ratios or the Pythagorean theorem shows the hypotenuse to have a length of 2).
Since the angle measure we’re looking for is the one across from the side with a length of 1, we’re dealing with a 30 degree angle. Now all that remains is to convert 30 degrees into radians, as the problem requests.
Degrees times Pi over 180 equals radians. So we have 30*Pi / 180 = radians. Solving for the unknown, radians, gives Pi/6. The answer to the problem is 6.
* * *
These are just a couple examples of SAT geometry problems. Remember that all geometry problems on the SAT are secretly algebra problems. A facility with algebra (and a knowledge of the 6 or so geometry concepts enumerated in the previous section) should be enough to build your SAT geometry confidence.
* * *
That’s it! For more college application advice, as well as a wealth of SAT and ACT prep tips, check out the rest of our blog. Looking for 1-on-1 ACT or SAT prep tutoring? Want to join an SAT or ACT group class? Contact us today!